Selection Sort

Sorting an array containing N integers using the Selection Sort algorithm. Write a program that performs this sorting operation.

Example:-

Given the array: [64, 25, 12, 22, 11]

• Pass 1: Find the smallest (11) and swap with the first element → [11, 25, 12, 22, 64]
• Pass 2: Find the smallest (12) in the remaining →[11, 12, 25, 22, 64]
• Pass 3: Find the smallest (22) → [11, 12, 22, 25, 64]
• Pass 4: Find the smallest (25) → [11, 12, 22, 25, 64]
• The array is now sorted.:

Solution

Note: Before diving into the solution, give it a try yourself!

Approach:

Here’s a breakdown of how the Selection Sort algorithm works:

1) Define the Unsorted Range: An outer loop (let's call it i) marks the starting point of the unsorted section of the array. This loop runs from 0 t0 n−1. For example, when i is 0, the entire array is unsorted; when i is 1, the unsorted range starts from index 1, and so on.

2) Identify the Minimum Element: In each iteration of the outer loop, an inner loop searches for the smallest element within the current unsorted portion of the array.

3) Swap Elements: After locating the smallest element, it is swapped with the first element of the unsorted section (the element at index i).

4) Increment the Range: After each pass, the portion of the array up to index i becomes sorted. Thus, i is incremented by 1, which reduces the unsorted range for the next iteration. The inner loop, denoted by j, is responsible for finding the minimum element within the range from i to n−1.

Dry run:

The following dry run will clarify the concepts:

Assume the given array is: {7, 5, 9, 2, 8}

Outer loop iteration 1:
The range will be the whole array starting from the 1st index as this is the first iteration. The minimum element of this range is 2(found using the inner loop).

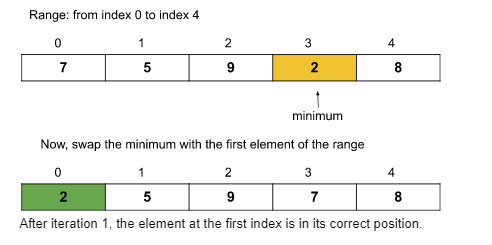
Outer loop iteration 2:
The range will be from the [2nd index to the last index] as the array is sorted up to the first index. The minimum element of this range is 5(found using the inner loop).

Outer loop iteration 3:
The range will be from the [3rd index to the last index]. The minimum element of this range is 7(found using the inner loop).

Outer loop iteration 4:
The range will be from the [4th index to the last index]. The minimum element of this range is 8(found using the inner loop).

So, after 4 iterations(i.e. n-1 iterations where n = size of the array), the given array is sorted.

CODE  

#include<iostream>

using namespace std;
void selection_sort(int arr[], int n) {
  // selection sort
  for (int i = 0; i < n - 1; i++) {
    int mini = i;
    for (int j = i + 1; j < n; j++) {
      if (arr[j] < arr[mini]) {
        mini = j;
      }
    }
    int temp = arr[mini];
    arr[mini] = arr[i];
    arr[i] = temp;
  }

  cout << "After selection sort: " << "\n";
  for (int i = 0; i < n; i++) {
    cout << arr[i] << " ";
  }
  cout << "\n";

}
int main() {
  int arr[] = {13,46,24,52,20,9};
  int n = sizeof(arr) / sizeof(arr[0]);
   cout << "Before selection sort: " << "\n";
   for (int i = 0; i < n; i++) {
    cout << arr[i] << " ";
  }
  cout << "\n";
  selection_sort(arr, n);
  return 0;
  }

OUTPUT  

Before selection sort:
13 46 24 52 20 9

After selection sort:
9 13 20 24 46 52

Time Complexity: O(N²) for the best, worst, and average cases.

Reason: The outer loop, indexed by i, runs from 0 to n-2, resulting in n-1 iterations. For each i, the inner loop indexed by j runs from i to n-1. Specifically, for i = 0, the inner loop runs n-1 times; for i = 1, it runs n-2 times; and so forth. The total number of steps can be expressed as:
(n−1)+(n−2)+(n−3)+…+3+2+1

This summation is approximately the sum of the first n natural numbers, given byn(n+1)/2. Therefore, the precise time complexity can be simplified to O(n*n).Here, n refers to the size of the array.

Space Complexity: O(1)